题目内容
14.某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
分析 (1)设每件乙种商品的价格为x元,则每件甲种商品的价格为(x+10)元,根据数量=总价÷单价结合用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设购买y件甲种商品,则购买(50-y)件乙种商品,根据总价=单价×购买数量结合投入的经费不超过3200元,即可得出关于y的一元一次不等式,解之即可得出y的取值范围,取其内的最大正整数即可.
解答 解:(1)设每件乙种商品的价格为x元,则每件甲种商品的价格为(x+10)元,
根据题意得:$\frac{350}{x+10}$=$\frac{300}{x}$,
解得:x=60,
经检验,x=60是原方程的解,
∴x+10=70.
答:每件乙种商品的价格为60元,每件甲种商品的价格为70元.
(2)设购买y件甲种商品,则购买(50-y)件乙种商品,
根据题意得:70y+60(50-y)≤3200,
解得:x≤20.
答:最多可购买20件甲种商品.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据数量=总价÷单价,列出关于x的分式方程;(2)根据总价=单价×购买数量,列出关于y的一元一次不等式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2.下列依次给出的点的坐标(0,3),(1,1),(2,-1),(3,-3),…,依此规律,则第2017个点的坐标为( )
| A. | (2017,-2015) | B. | (2016,-2014) | C. | (2016,-4029) | D. | (2016,-4031) |
9.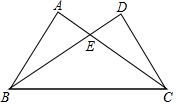 如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
 如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )| A. | ∠D=60° | B. | ∠DBC=40° | C. | AC=DB | D. | BE=10 |
19.下列图形中,∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
6.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
①3cm,4cm,5cm
②8cm,7cm,15cm
③13cm,12cm,20cm
④5cm,5cm,11cm.
①3cm,4cm,5cm
②8cm,7cm,15cm
③13cm,12cm,20cm
④5cm,5cm,11cm.
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
3. 如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )
如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )
 如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )
如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )| A. | 140° | B. | 150° | C. | 160° | D. | 170° |
4.设n为正整数,且n<$\sqrt{62}$<n+1,则n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,∠A=2∠ABC,BD平分∠ABC,且AD∥BC,请运用所学知识,求∠ADB的度数.
如图,∠A=2∠ABC,BD平分∠ABC,且AD∥BC,请运用所学知识,求∠ADB的度数.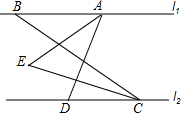 如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.