题目内容
2.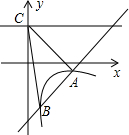 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
分析 (1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)利用两点间的距离公式求出AB的长,利用点到直线的距离公式求出点C到直线AB的距离,即可确定出三角形ABC面积.
解答 解:(1)把A(2,-1)代入反比例解析式得:-1=$\frac{m}{2}$,即m=-2,
∴反比例解析式为y=-$\frac{2}{x}$,
把B($\frac{1}{2}$,n)代入反比例解析式得:n=-4,即B($\frac{1}{2}$,-4),
把A与B坐标代入y=kx+b中得:$\left\{\begin{array}{l}{2k+b=-1}\\{\frac{1}{2}k+b=-4}\end{array}\right.$,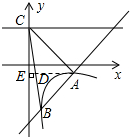
解得:k=2,b=-5,
则一次函数解析式为y=2x-5;
(2)∵A(2,-1),B($\frac{1}{2}$,-4),直线AB解析式为y=2x-5,
∵C(0,2),直线BC解析式为y=-12x+2,
将y=-1代入BC的解析式得x=$\frac{1}{4}$,则AD=2-$\frac{1}{4}$=$\frac{7}{4}$.
∵xC-xB=2-(-4)=6,
∴S△ABC=$\frac{1}{2}$×AD×(yC-yB)=$\frac{1}{2}$×$\frac{7}{4}$×6=$\frac{21}{4}$.
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
7.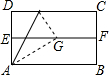 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
11.若x1,x2是一元二次方程x2-2x-1=0的两个根,则x12-x1+x2的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
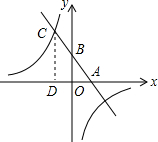 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=$\frac{39}{2}$. 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.
如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.