题目内容
17. 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.
如图,直线a∥b,∠1=45°,∠2=30°,则∠P=75°.
分析 过P作PM∥直线a,求出直线a∥b∥PM,根据平行线的性质得出∠EPM=∠2=30°,∠FPM=∠1=45°,即可求出答案.
解答 解: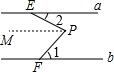
过P作PM∥直线a,
∵直线a∥b,
∴直线a∥b∥PM,
∵∠1=45°,∠2=30°,
∴∠EPM=∠2=30°,∠FPM=∠1=45°,
∴∠EPF=∠EPM+∠FPM=30°+45°=75°,
故答案为:75.
点评 本题考查了平行线的性质的应用,能正确根据平行线的性质进行推理是解此题的关键,注意:两直线平行,内错角相等.

练习册系列答案
相关题目
8.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线经过点(2,3) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
5. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )| A. | $\sqrt{5}$ | B. | $\frac{13}{6}$ | C. | 1 | D. | $\frac{5}{6}$ |
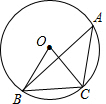 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.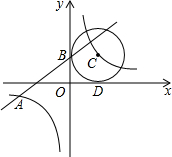 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B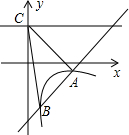 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.