若x1.x2是一元二次方程x2-2x-1=0的两个根.则x12-x1+x2的值为( )A．-1B．0C．2D．3 题目和参考答案——青夏教育精英家教网—

题目内容

11．若x₁，x₂是一元二次方程x²-2x-1=0的两个根，则x₁²-x₁+x₂的值为（　　）

A．

-1

B．

C．

D．

分析由根与系数的关系得出“x₁+x₂=2，x₁•x₂=-1”，将代数式x₁²-x₁+x₂变形为x₁²-2x₁-1+x₁+1+x₂，套入数据即可得出结论．

解答解：∵x₁，x₂是一元二次方程x²-2x-1=0的两个根，
∴x₁+x₂=-$\frac{b}{a}$=2，x₁•x₂=$\frac{c}{a}$=-1．
x₁²-x₁+x₂=x₁²-2x₁-1+x₁+1+x₂=1+x₁+x₂=1+2=3．
故选D．

点评本题考查了根与系数的关系，解题的关键是利用根与系数的关系找出两根之积与两根之和．本题属于基础题，难度不大，解决该题型题目时，根据根与系数的关系，找出两根之和与两根之积是关键．

练习册系列答案

2．

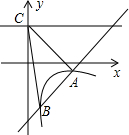如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$（x＞0）的图象交于A（2，-1），B（$\frac{1}{2}$，n）两点，直线y=2与y轴交于点C．
（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积．

x³-x²=x

x³•x²=x⁶

（x³）²=x⁵

6．计算：|-3|+$\sqrt{3}$tan30°-$\sqrt{12}$-（2016-π）⁰．

16．下列图形中不是轴对称图形的是（　　）

3．化简：（a+1-$\frac{3}{a-1}$）•$\frac{2a-2}{a+2}$．

6．已知在△ABC中，∠ABC=45°，AD⊥BC，且BD=4，高AD上有一动点E（点E不与点A、点D重合），联结BE并延长与边AC相交于点F．
（1）当点E为AD中点，且BF⊥AC时，求AF；
（2）当DC=3，设DE=x，AF=y，请建立y与x的函数关系式，并写出定义域；
（3）在（2）的条件下，当△AEF为等腰三角形时，求DE的长．

（-2^-2）³=-$\frac{1}{6}$

D．

-（2^-2）³=$\frac{3}{4}$

试题分类