题目内容
14.已知关于x的一元二次方程x2-6x+(2m+1)=0有实数根.(1)求m的取值范围;
(2)如果方程的两个实数根为x1,x2,且2x1x2+x1+x2≥20,求m的取值范围.
分析 (1)根据判别式的意义得到△=(-6)2-4(2m+1)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=6,x1x2=2m+1,再利用2x1x2+x1+x2≥20得到2(2m+1)+6≥20,然后解不等式和利用(1)中的结论可确定满足条件的m的取值范围.
解答 解:(1)根据题意得△=(-6)2-4(2m+1)≥0,
解得m≤4;
(2)根据题意得x1+x2=6,x1x2=2m+1,
而2x1x2+x1+x2≥20,
所以2(2m+1)+6≥20,解得m≥3,
而m≤4,
所以m的范围为3≤m≤4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根与系数的关系.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | (a2)3=a5 | B. | (-2a)2=-4a2 | C. | m3•m2=m6 | D. | a6÷a2=a4 |
5. 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
 如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )| A. | $\sqrt{5}$ | B. | $\frac{13}{6}$ | C. | 1 | D. | $\frac{5}{6}$ |
19.下列计算正确的是( )
| A. | x3-x2=x | B. | x3•x2=x6 | C. | x3÷x2=x | D. | (x3)2=x5 |
10.某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )
| 人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
| 金额(元) | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
| A. | 极差是195000 | B. | 中位数是15000 | C. | 众数是15000 | D. | 平均数是15000 |
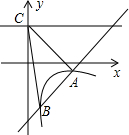 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.