题目内容
12.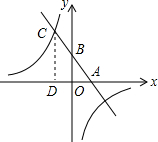 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤$\frac{n}{x}$的解集.
分析 (1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可解决问题.
(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.
解答 解:(1)∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥OA,
∴DC∥OB,
∴$\frac{OB}{CD}$=$\frac{AO}{AD}$,
∴$\frac{6}{CD}$=$\frac{3}{5}$,
∴CD=10,
∴点C坐标(-2,10),B(0,6),A(3,0),
∴$\left\{\begin{array}{l}{b=6}\\{3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴一次函数为y=-2x+6.
∵反比例函数y=$\frac{n}{x}$经过点C(-2,10),
∴n=-20,
∴反比例函数解析式为y=-$\frac{20}{x}$.
(2)由$\left\{\begin{array}{l}{y=-2x+6}\\{y=-\frac{20}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=10}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$,
故另一个交点坐标为(5,-4).
(3)由图象可知kx+b≤$\frac{n}{x}$的解集:-2≤x<0或x≥5.
点评 本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围,属于中考常考题型.

 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | (a2)3=a5 | B. | (-2a)2=-4a2 | C. | m3•m2=m6 | D. | a6÷a2=a4 |
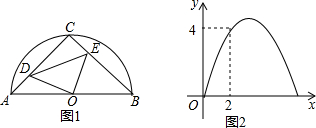
 如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.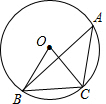 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
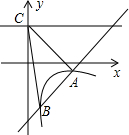 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A(2,-1),B($\frac{1}{2}$,n)两点,直线y=2与y轴交于点C.