题目内容
20.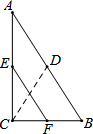 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
分析 根据三角形中位线定理证明EF=$\frac{1}{2}$AB,根据直角三角形斜边上的中线等于斜边的一半证明CD=$\frac{1}{2}$AB,得到答案.
解答 解:∵E、F分别为AC、BC的中点,
∴EF=$\frac{1}{2}$AB=$\sqrt{3}$,
在Rt△ABC中,D是AB的中点,
∴CD=$\frac{1}{2}$AB=$\sqrt{3}$,
∴CD=EF,
故选:C.
点评 本题考查的是三角形中位线定理和直角三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半和直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
5.用同样大小的黑色五角星按如图所示的方式摆图案,按照这样的规律摆下去,第7个图案需要的黑色五角星的个数是( )


| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
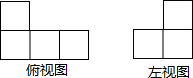 如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.
如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.