题目内容
11.若2a+b=12,其中a≥0,b≥0,又P=3a+2b.试确定P的最小值和最大值.分析 由2a+b=12,其中a≥0,b≥0,可知0≤a≤6,由2a+b=12得;b=12-2a,然后代入P=3a+2b得;p=24-a,最后根据a的范围即可求得p的范围.
解答 解:∵2a+b=12,a≥0,b≥0,
∴2a≤12.
∴a≤6.
∴0≤a≤6.
由2a+b=12得;b=12-2a,
将b=12-2a代入P=3a+2b得:
p=3a+2(12-2a)
=24-a.
当a=0时,P有最大值,最大值为p=24.
当a=6时,P有最小值,最小值为P=18.
点评 本题主要考查的解一元一次不等式和整式的加减,由已知条件确定出a的范围以及得出p=24-a是解题的关键.

练习册系列答案
相关题目
1.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 2,2,3 | B. | 3,4,5 | C. | 5,12,13 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
2.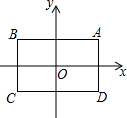 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
3.下列各式计算正确的是( )
| A. | 2x2y+3xy=5x3y2 | B. | (2x2y)3=8x6y3 | C. | 2x2y•3xy=6x2y | D. | 2x2y÷3xy=$\frac{2}{3}$xy |
20.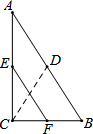 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
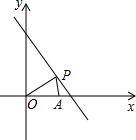 已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).
已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).