题目内容
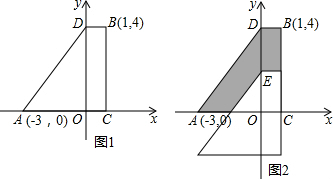
15.如图1,四边形ABCD是某市凌河休闲广场一个供市民休息和观赏的看台侧面示意图.已知:在四边形ABCD中,AB∥CD中,AB∥CD,AB=2米,BC⊥DC,∠ADC=30°.从底边DC上点E测得点B的仰角∠BEC=60°,且DE=6米.(1)求AD的长度;
(2)如图2,为了避免白天市民在看台AB和AD的位置受到与水平面成45°角的光线照射,想修建一个遮阳篷,求这个遮阳篷的宽度HG是多少米?(计算结果都保留根号)
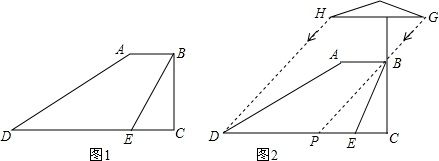
分析 (1)作BF⊥AD角CD于F,证明四边形ABFD是平行四边形,得到DF=2,BC=x,在Rt△BCE中,根据正切求出CE,列方程求出x,得到答案;
(2)证明四边形DHGP是平行四边形,得到HG=DP,求出DP即可.
解答  解:(1)如图1,作BF⊥AD角CD于F,
解:(1)如图1,作BF⊥AD角CD于F,
又∵AB∥CD,
∴四边形ABFD是平行四边形,
∴AB=DF=2,AD∥BF,
∴∠BFE=∠D=30°,EF=DE-DF=4,
在Rt△BCF中,设BC=x米,
则BF=2x,CF=$\sqrt{3}$x,
在Rt△BCE中,∠BEC=60°,
∴CE=$\frac{BC}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
∴EF=CF-CE=$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=4,
解得:x=2$\sqrt{3}$,
∴AD=BF=2x=4$\sqrt{3}$;
(2)∵DH∥PG,HG∥PD,
∴四边形DHGP是平行四边形,
∴HG=DP,
由题意得,∠BPE=45°,
在Rt△BCE中,BC=CP=2$\sqrt{3}$,
由(1)知,EC=2,∴PE=PC-EC=2$\sqrt{3}$-2,
∵HG=DP=DE-PE,
∴HG=6-(2$\sqrt{3}$-2)=8-2$\sqrt{3}$.
点评 本题考查的是解直角三角形的应用,正确作出辅助线、灵活应用锐角三角函数的概念是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列各式计算正确的是( )
| A. | 2x2y+3xy=5x3y2 | B. | (2x2y)3=8x6y3 | C. | 2x2y•3xy=6x2y | D. | 2x2y÷3xy=$\frac{2}{3}$xy |
20.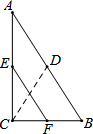 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
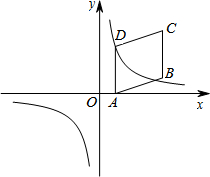 如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=$\frac{m}{x}$的图象经过点D.点P是一次函数y=kx+4-4k(k≠0)的图象与该反比例函数图象的一个公共点.
如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=$\frac{m}{x}$的图象经过点D.点P是一次函数y=kx+4-4k(k≠0)的图象与该反比例函数图象的一个公共点.
 如图,在平面直角坐标系中,直线y=-4x+4与x轴,y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m的值为$\frac{15}{4}$.
如图,在平面直角坐标系中,直线y=-4x+4与x轴,y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m的值为$\frac{15}{4}$.