题目内容
10.在平面直角坐标系中,点P(a-4,a)是第二象限内的点,则a的取值范围是0<a<4.分析 根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.
解答 解:∵点P(a-4,a)是第二象限内的点,
∴$\left\{\begin{array}{l}{a-4<0}\\{a>0}\end{array}\right.$,
解得0<a<4.
故答案为:0<a<4.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列从左到右的变形是因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | (a-3)(a+7)=a2+4a-21 | ||
| C. | x2+x+$\frac{1}{4}$=(x+$\frac{1}{2}$)2 | D. | 3x3-6x2+4=3x2(x-2)+4 |
1.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 2,2,3 | B. | 3,4,5 | C. | 5,12,13 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
18.已知y=(m-3)x|m|-2+1是一次函数,则m的值是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | ±2 |
15.在课外活动时间,小王、小丽、小华做“互相踢毽子”游戏,毽子从一人传到另一人就记为踢一次.若从小丽开始,经过两次踢毽后,毽子踢到小华处的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
2.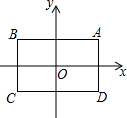 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的二元一次方程$\left\{\begin{array}{l}{mnx+y=2n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
20.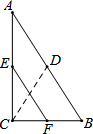 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2$\sqrt{3}$,则DC和EF的大小关系是( )| A. | DC>EF | B. | DC<EF | C. | DC=EF | D. | 无法比较 |
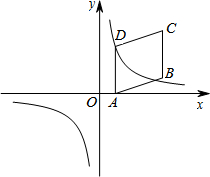 如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=$\frac{m}{x}$的图象经过点D.点P是一次函数y=kx+4-4k(k≠0)的图象与该反比例函数图象的一个公共点.
如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=$\frac{m}{x}$的图象经过点D.点P是一次函数y=kx+4-4k(k≠0)的图象与该反比例函数图象的一个公共点.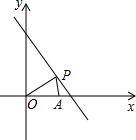 已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).
已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).