题目内容
13.在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,求证:AB2=AC•AE+BC•BD.分析 记AD与BE交点为H,连接CH并延长交AB于点F,由AD⊥BC、BE⊥AC知CH⊥AB,从而可得△ABE∽△ACF、△BDA∽△BFC,根据相似三角形性质得AB•AF=AE•AC、AB•BF=BC•BD,两式相加即可得证.
解答 证明:如图,记AD与BE交点为H,连接CH并延长交AB于点F,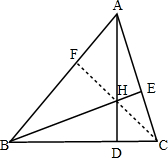
∵AD⊥BC于D,BE⊥AC于E,
∴BE、AD的交点H是△ABC的垂心,
∴CH⊥AB,
∴∠AFC=∠AEB=90°,
又∵∠BAE=∠CAF,
∴△ABE∽△ACF,
∴$\frac{AB}{AE}=\frac{AC}{AF}$,即AB•AF=AE•AC,
同理,△BDA∽△BFC,
∴$\frac{AB}{BC}=\frac{BD}{BF}$,即AB•BF=BC•BD,
∴AC•AE+BC•BD=AB•AF+AB•BF
=AB(AF+BF)
=AB•AB
=AB2,
即AB2=AC•AE+BC•BD.
点评 本题主要考查相似三角形的性质和判定及三角形的垂心,构建相似三角形将待求线段根据相似形的性质联系到一起是解题的关键.

练习册系列答案
相关题目
3.若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数,则符合条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.分式$\frac{x}{x-1}$+$\frac{1}{1-x}$可化简为( )
| A. | $\frac{x+1}{x-1}$ | B. | 1 | C. | -1 | D. | $\frac{x+1}{1-x}$ |
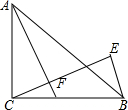 如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.
如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.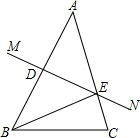 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.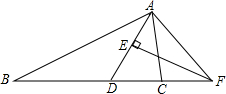 如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.