题目内容
4.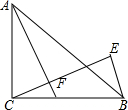 如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.
如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.
分析 由已知条件得出∠ACF=∠CBE,由AAS证明△AFC≌△CEB,得出AF=CE,CF=BE,证明△AFC∽△ACFD,得出对应边成比例CD:AC=CF:AF,由已知条件得出AC=2CD,即可得出结果.
解答 解:∵∠ACB=90°,AC=BC,BE⊥CF,
∴∠ACD=∠E=90°,∠ACF=∠CBE,
在△AFC和△CEB中,$\left\{\begin{array}{l}{∠AFC=∠E}&{\;}\\{∠ACF=∠CBE}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△AFC≌△CEB(AAS),
∴AF=CE,CF=BE,
∵CF⊥AD,∠ACB=90°,
∴△AFC∽△ACFD,
∴CD:AC=CF:AF,
∵D为BC的中点,
∴CD=BD,AC=BC,
∴AC=2CD,
∴CF:AF=BE:AF=CD:AC=1:2.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质;证明三角形相似和三角形全等是解决问题的关键.

练习册系列答案
相关题目




 ?ABCD中,有一点P,使∠APD=∠ADP.连接AP、BP、DP、CP,求证:∠PAD=∠PCB.
?ABCD中,有一点P,使∠APD=∠ADP.连接AP、BP、DP、CP,求证:∠PAD=∠PCB.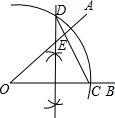 如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.
如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.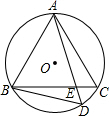 如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.
如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.