题目内容
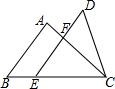
2．
小亮要判断△ABC的面积是△DBC的面积的几倍，现仅有一把有刻度的直尺，则至少需要测量的次数是（ ）| A． | 1次 | B． | 2次 | C． | 3次 | D． | 4次 |
分析 连接AD交BC于M，一次测量AM和AD的长（在同一直线上，可以一次就测出），然后求出DM，再根据等高的三角形的面积的比等于底边的比求解．
解答 
解：连接AD交BC于M，一次测量AM（AD）即可得AD，AM长，
即可算出DM长，由AM：DM=AP：DQ，即可求出△ABC的面积是△DBC的面积的几倍．
故只量一次．
故选A．
点评 本题考查了三角形的面积，主要利用了等底的三角形的面积的比等于高线的比．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB=6，EF=4，则DF的长是（ ）
10．
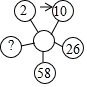如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（ ）
如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（ ）| A． | 119 | B． | 120 | C． | 121 | D． | 122 |
17．已知两个整数a，b，满足0＜b＜a＜10，且$\frac{9a}{a+b}$是整数，那么数对（a，b）有（ ）
| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
7．
如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则$\frac{GH}{EF}$的值是（ ）
如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则$\frac{GH}{EF}$的值是（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |
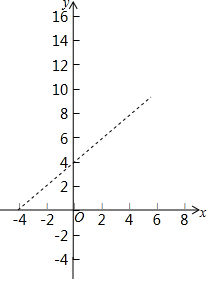如图，已知 A（-4，0），B（0，4），现以A点为位似中心，相似比为4：9，将OB向右侧放大，B点的对应点为C．
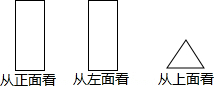已知某几何体从正面和左面看都是大小相同的长方形，从上面看是一个等边三角形，如图所示．