题目内容
12.解下列方程组:(1)$\left\{\begin{array}{l}{y=2x-3}\\{3x+2y=8}\end{array}\right.$(用代入消元法)
(2)$\left\{\begin{array}{l}{3x-y=5}\\{5x+2y=23}\end{array}\right.$(用加减消元法)
分析 (1)此方程采用代入消元法最简单,可以直接把①代入②,即可消去未知数y,解方程即可求得;
(2)将方程①×2+②消去未知数y,解方程即可求得.
解答 解:(1)在$\left\{\begin{array}{l}{y=2x-3}&{①}\\{3x+2y=8}&{②}\end{array}\right.$中,
将①代入②得:3x+2(2x-3)=8,
解得:x=2,
将x=2代入①得:y=2×2-3=1,
故方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-y=5}&{①}\\{5x+2y=23}&{②}\end{array}\right.$,
①×2+②,得:11x=33,
解得:x=3,
将x=3代入①,得:9-y=5,
解得:y=4,
故方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.直线y=2x+1与直线y=-3x+6交于点(a,b),则$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组( )的解.
| A. | $\left\{\begin{array}{l}{y=2x+1}\\{y=-3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=2x+1}\\{y=-3x+6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=2x+1}\\{y=3x+6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=2x-1}\\{y=-3x+6}\end{array}\right.$ |
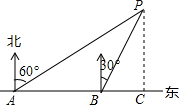 如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.
如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.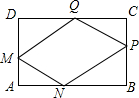 在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.
在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.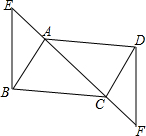 已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)
已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)