题目内容
11.对于二次函数y=x2-2mx-3有下列说法:①如果当x≤1时y随x的增大而减小,则m=1;
②如果它的图象与x轴的两交点的距离是4,则m=±1;
③如果将它的图象向左平移3个单位后函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2015时的函数值相等,则当x=2016时的函数值为-3.
其中正确的说法是②④.
分析 首先用m表示出二次函数图象的对称轴,然后结合图象的单调性即可对①作出判断;
用m表示出图象与x轴的两交点的距离,再解出m的值即可对②作出判断;
先把二次函数y=x2-2mx-3化为顶点坐标式,根据函数最小值为4即可求出m的值,进而对③作出判断;
先求出对称轴为x=1008,然后可知x=2016时的函数值与x=0值相等,据此对④作出判断.
解答 解:①∵当x≤1时y随x的增大而减小,
∴函数的对称轴x=-$\frac{-2m}{2}$≥1在直线x=1的右侧(包括与直线x=1重合),
∴m≥1,故本选项错误;
②令y=x2-2mx-3=0,x1+x2=2m,x1x2=-3,
|x1-x2|2=(x1+x2)2-4x1x2=4m2+12=16,
解得m=±1,故本选项正确;
③二次函数y=x2-2mx-3=(x-m)2-m2-3,
当图象向左平移3个单位后的函数的最小值是-4,
则-m2-3=-4,
解得m=±1,故本选项错误;
④当x=1时的函数值与x=2015时的函数值相等,
则二次函数图象对称轴为x=1008,
则x=2016时的函数值与x=0值相等,
则当x=2016时的函数值为-3,故本选项正确;
故答案为②④.
点评 本题主要考查了二次函数的性质的知识,解答本题的关键是要掌握二次函数图象的对称轴,开口方向、函数的单调性等知识,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.根据表格的对应值得到函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象与x轴有一个交点的横坐标x的范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| y=ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
| A. | x<3.23 | B. | 3.23<x<3.24 | C. | 3.24<x<3.25 | D. | 3.25<x<3.26 |
1. 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )| A. | 20° | B. | 22° | C. | 24° | D. | 26° |
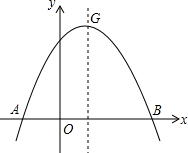 如图,抛物线y=-x2+tx+2t2(t>0)与x轴交于A、B两点,点A在点B的左边,抛物线顶点为G.
如图,抛物线y=-x2+tx+2t2(t>0)与x轴交于A、B两点,点A在点B的左边,抛物线顶点为G.