题目内容
20.直角三角形的两直角边之比为$\sqrt{2}$:1,斜边长是2$\sqrt{3}$,则此三角形的面积为2$\sqrt{2}$.分析 设直角三角形的两条直角边长分别为$\sqrt{2}$x、x,由勾股定理得出方程,解方程求出直角三角形的两条直角边长,即可求出直角三角形的面积.
解答 解:设直角三角形的两条直角边长分别为$\sqrt{2}$x、x,
由勾股定理得:($\sqrt{2}$x)2+x2=(2$\sqrt{3}$)2,
解得:x=$\sqrt{4}$=2,
∴直角三角形的两条直角边长分别为2$\sqrt{2}$、2;
∴直角三角形的面积=$\frac{1}{2}$×2$\sqrt{2}$×2=2$\sqrt{2}$;
故答案为:2$\sqrt{2}$.
点评 本题考查了勾股定理、直角三角形面积的计算方法;熟练掌握勾股定理,由勾股定理得出方程求出两条直角边长是解决问题的关键.

练习册系列答案
相关题目
10.下列说法中正确的是( )
| A. | 在等式ax=bx两边除以x,可得a=b | B. | 由等式a2=b2,一定有a=b | ||
| C. | 在等式$\frac{a}{3}=\frac{b}{3}$两边除以3,得到a=b | D. | 由等式5x=4x+1,可得x=1 |
9.22016×(-2)2016的计算结果是( )
| A. | 0 | B. | -24032 | C. | 24032 | D. | -44032 |
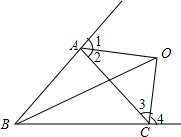 已知,如图,∠1=∠2,∠3=∠4,A0、CO相交于点0.
已知,如图,∠1=∠2,∠3=∠4,A0、CO相交于点0.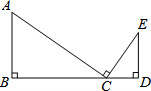 已知:如图,AC⊥CE,AB⊥BD,ED⊥BD,BC=DE,求证:△ABC≌△CDE.
已知:如图,AC⊥CE,AB⊥BD,ED⊥BD,BC=DE,求证:△ABC≌△CDE.