题目内容
19.计算或解方程(1)$(x-1{)^0}+{(\frac{1}{2})^{-1}}+|{5-\sqrt{27}}|-2\sqrt{3}$
(2)$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})-{(\sqrt{5}-\sqrt{2})^2}$
(3)x2-3x-1=0
(4)9(x-2)2=4(x+1)2.
分析 (1)根据零指数幂、负整数指数幂和绝对值的意义得到原式=1+2+3$\sqrt{3}$-5-2$\sqrt{3}$,然后合并即可;
(2)根据平方差公式和完全平方公式计算;
(3)利用求根公式解方程;
(4)两边开方得3(x-2)=±2(x+1),然后解两个一次方程即可.
解答 解:(1)原式=1+2+3$\sqrt{3}$-5-2$\sqrt{3}$
=$\sqrt{3}$-2;
(2)原式=3-2-(5-2$\sqrt{10}$+2)
=1-7+2$\sqrt{10}$
=-6+2$\sqrt{10}$;
(3)△=(-3)2-4×1×(-1)=13,
x=$\frac{3±\sqrt{13}}{2×1}$,
所以x1=$\frac{3-\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$;
(4)3(x-2)=±2(x+1),
所以x1=8,x2=$\frac{4}{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解一元二次方程.

练习册系列答案
相关题目
9.22016×(-2)2016的计算结果是( )
| A. | 0 | B. | -24032 | C. | 24032 | D. | -44032 |
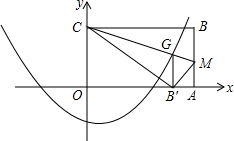 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.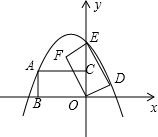 如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且点B(-$\sqrt{3}$,0),C(0,1),矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且点B(-$\sqrt{3}$,0),C(0,1),矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D. 如图所示,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠A=40°,BO是△ABD的角平分线,求∠BDC.
如图所示,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠A=40°,BO是△ABD的角平分线,求∠BDC.