题目内容
16.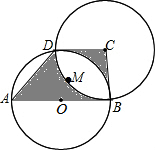 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:(1)线段AB与线段DC都分别垂直于BC;
(2)AB=2CD,$\widehat{DMB}$是以点C为圆心的圆弧.
请问如图中阴影部分的面积与圆O的面积之比是多少?
分析 连结BD,设⊙O的半径为r,则OB=BC=CD=r.先求出梯形ABCD内部空白部分的面积,那么图中阴影部分的面积=S梯形ABCD-S空白,再求出⊙O的面积=πr2,进而得到图中阴影部分的面积与⊙O的面积之比.
解答 解: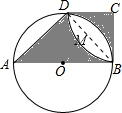 如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.
如图,连结BD,设⊙O的半径为r,则OB=BC=CD=r.
∵梯形ABCD内部空白部分的面积=2(S扇形DCB-S△DCB)=2×($\frac{90π•{r}^{2}}{360}$-$\frac{1}{2}$r2)=($\frac{1}{2}$π-1)r2,
∴图中阴影部分的面积=S梯形ABCD-S空白=$\frac{1}{2}$(r+2r)•r-($\frac{1}{2}$π-1)r2=($\frac{5}{2}$-$\frac{1}{2}$π)r2,
又∵⊙O的面积=πr2,
∴图中阴影部分的面积与⊙O的面积之比为$\frac{\frac{5-π}{2}{r}^{2}}{π{r}^{2}}$=$\frac{5-π}{2π}$.
点评 本题考查了扇形面积的计算,准确作出辅助线,求出梯形ABCD内部空白部分的面积是解题的关键.

练习册系列答案
相关题目
6.我们规定以下三种变换:
(1)f(a,b)=(-a,b).如:f(1,3)=(-1,3);
(2)g(a,b)=(b,a).如:g(1,3)=(3,1);
(3)h(a,b)=(-a,-b).如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),
求f(h(5,-3))=( )
(1)f(a,b)=(-a,b).如:f(1,3)=(-1,3);
(2)g(a,b)=(b,a).如:g(1,3)=(3,1);
(3)h(a,b)=(-a,-b).如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),
求f(h(5,-3))=( )
| A. | (5,-3) | B. | (-5,3) | C. | (5,3) | D. | (3,5) |
11.如果三角形的一个外角的平分线平行于三角形的一边,那么这个三角形是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
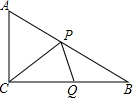 如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,
如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,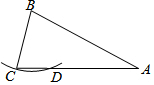 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为1.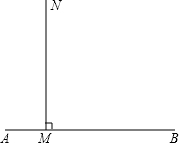 已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.
已知如图:射线MN⊥AB于点M,点C从M出发,以1cm/s的速度沿射线MN运动,AM=1,MB=4,设运动时间为ts,①当△ABC为等腰三角形时,求t的值;②当△ABC为直角三角形时,求t的值;③点C在运动的过程中,若△ABC为钝角三角形,则t的取值范围是0<t<2;若△ABC为锐角三角形,则t的取值范围是t>2.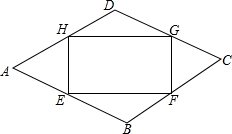 如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.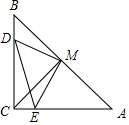 如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.
如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.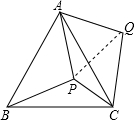 P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.
P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.