题目内容
8.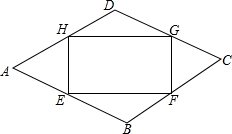 如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH,∠A=60°.设AE=x,四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,则菱形边长为4.
分析 根据菱形的性质结合等边三角形的判定与性质得出△AEH是等边三角形,进而表示出BE的长,即可得出答案.
解答  解:过点B作BN⊥EF于点N,
解:过点B作BN⊥EF于点N,
∵四边形ABCD是菱形,
∴AB=BC=DC=AD,
∵BE=BF=DG=DH,
∴AH=AE,EN=NF,
又∵∠A=60°,
∴△AEH是等边三角形,
∴AE=HE=x,
∵四边形EFGH的面积为s与边AE的关系为s=-$\sqrt{3}{x}^{2}$+4$\sqrt{3}$x,
∴EF=-$\sqrt{3}$x+4$\sqrt{3}$,
∴NE=$\frac{-\sqrt{3}x+4\sqrt{3}}{2}$,
∵∠AEH=60°,∠HEF=90°,
∴∠FEB=30°,
故cos30°=$\frac{EN}{BE}$=$\frac{\sqrt{3}}{2}$,
则BE=-x+4,
故AB=AE+BE=x-x+4=4,
即菱形的边长为:4.
故答案为:4.
点评 此题主要考查了菱形的性质以及等边三角形的判定与性质和矩形面积求法等知识,正确表示出BE的长是解题关键.

练习册系列答案
相关题目
18.10月23日新闻网报道,河北2015年各地取暖标准出炉,衡水、邢台等地取暖费标准不变.慧慧家在衡水,欣欣家在邢台,慧慧家的建筑面积与欣欣家的相同,慧慧家和欣欣家2015年所交的取暖费分别为1995元和1890元,如邢台居民每平方米取暖费的价钱比衡水的便宜1元,则衡水居民每平米米取暖费的价钱为( )
| A. | 20元 | B. | 19元 | C. | 18元 | D. | 17元 |
3.一元二次方程x2+x-1=0 的根的情况为( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
13.下列函数关系不是一次函数的是( )
| A. | 汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系 | |
| B. | 等腰三角形顶角y与底角x间的关系 | |
| C. | 高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系 | |
| D. | 一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系 |
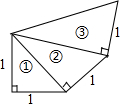 如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?
如图所示,一直按此规律进行下去,试求第10个直角三角形的斜边长为多少?第n个直角三角形的斜边长又为多少?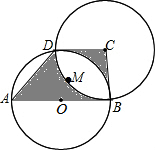 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中: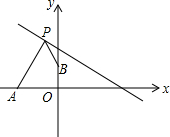 如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).
如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).