题目内容
5.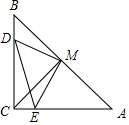 如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.
如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.
分析 欲求△MDE是等腰三角形,需证得MD=ME,可连接CM,证△BDM≌△CEM,即可得出结论.
解答  解:△MDE是等腰三角形,理由如下:
解:△MDE是等腰三角形,理由如下:
连接CM;如图所示:
等腰Rt△ABC中,CM是斜边AB的中线,
∴CM=BM,∠B=∠ECM=45°;
在△BDM和△CEM中,$\left\{\begin{array}{l}{BM=CW}&{\;}\\{∠B=∠ECM}&{\;}\\{BD=CE}&{\;}\end{array}\right.$,
∴△BDM≌△CEM(SAS);
∴MD=ME,
即△MDE是等腰三角形.
点评 此题主要考查了等腰直角三角形的性质、全等三角形的判定和性质、等腰三角形的判定等知识.能够正确的构建出全等三角形是解答此题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.下列函数关系不是一次函数的是( )
| A. | 汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系 | |
| B. | 等腰三角形顶角y与底角x间的关系 | |
| C. | 高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系 | |
| D. | 一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系 |
14.据浙江电商网统计,2014年嘉兴市网络零售额678.89亿元,列全省第三.其中678.89亿元可用科学记数法表示为( )
| A. | 678.89×108元 | B. | 67.889×109元 | C. | 6.7889×109元 | D. | 6.7889×1010元 |
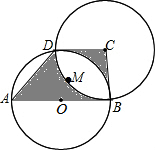 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中: 如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.
如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项.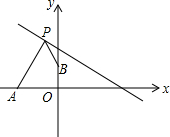 如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).
如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).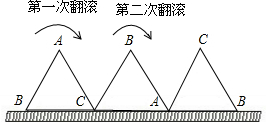 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.