题目内容
11. 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
分析 设B点坐标为(a,b),由矩形OABC的边AB的中点为F,则F点的坐标为(a,$\frac{b}{2}$),根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义得到S△OAF=S△OEC=$\frac{1}{2}$|k|=$\frac{1}{2}$a•$\frac{b}{2}$,则ab=2k,软件利用S矩形=S四边形OEBF+S△OAF+S△OEC得到ab=2+$\frac{1}{2}$k+$\frac{1}{2}$k,所以2k=k+2,再解一次方程即可.
解答 解:设B点坐标为(a,b),
∵矩形OABC的边AB的中点为F,
∴F点的坐标为(a,$\frac{b}{2}$),
∴S△OAF=S△OEC=$\frac{1}{2}$|k|=$\frac{1}{2}$a•$\frac{b}{2}$,
∴ab=2k,
∵S矩形=S四边形OEBF+S△OAF+S△OEC,
∴ab=9+$\frac{1}{2}$k+$\frac{1}{2}$k,
∴2k=k+2,
∴k=9.
故答案为:9.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
相关题目
16.下列命题中,属于真命题的是( )
| A. | 面积相等的三角形是全等三角形 | |
| B. | 同位角相等 | |
| C. | 若|a|=|b|,则a=b | |
| D. | 如果直线l1∥l2,直线l2∥l3,那么l1∥l3 |
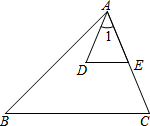 如图,在△ABC中,点E是AC上一点,DE∥BC,∠1=∠B,AD=AE.求证:AB=BC.
如图,在△ABC中,点E是AC上一点,DE∥BC,∠1=∠B,AD=AE.求证:AB=BC.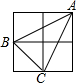 如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.
如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.