题目内容
2.计算:(1)(2$\sqrt{3}$+$\sqrt{6}$)(2$\sqrt{3}$-$\sqrt{6}$);
(2)(2$\sqrt{48}$-3$\sqrt{27}$)÷$\sqrt{6}$.
(3)($\frac{1}{5}$)-1+(1+$\sqrt{3}$)(1-$\sqrt{3}$)-$\sqrt{12}$
(4)(-1)2015+(π-3)0+($\frac{1}{2}$)-1-$\sqrt{(1-\sqrt{2})^{2}}$
(5)$\sqrt{3}$($\sqrt{2}$-$\sqrt{3}$)-$\sqrt{24}$-|$\sqrt{6}$-3|
(6)-22×$\sqrt{8}$+3$\sqrt{2}$(3-2$\sqrt{2}$)-(1-$\sqrt{18}$).
分析 (1)利用平方差公式计算;
(2)先化简合并,再算除法;
(3)先算负指数幂,利用平方差公式计算,再进一步合并即可;
(4)先算乘方、负指数幂、0指数幂,以及利用根式的化简,再进一步合并即可;
(5)(6)利用二次根式的运算方法计算化简,再进一步合并即可.
解答 解:(1)原式=12-6
=6;
(2)原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$;
(3)原式=5+1-3-2$\sqrt{3}$
=3-2$\sqrt{3}$;
(4)原式=-1+1+2-($\sqrt{2}$-1)
=3-$\sqrt{2}$;
(5)原式=$\sqrt{6}$-3-2$\sqrt{6}$-3+$\sqrt{6}$
=-6;
(6)原式=-8$\sqrt{2}$+9$\sqrt{2}$-12-1+3$\sqrt{2}$
=4$\sqrt{2}$-13.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
11.已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |

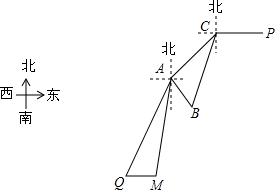 南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.
南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里. 如图,△ABC中AB=AC=10,BC=16.
如图,△ABC中AB=AC=10,BC=16. 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.