题目内容
20.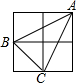 如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.
如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.
分析 易求△ABC的面积,再根据勾股定理可求出AB的长,进而根据面积公式即可求得AB边上的高的长.
解答 解:由题意可得S△ABC=4-$\frac{1}{2}$×2×1×2-$\frac{1}{2}$×1×1=1.5,
∵AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴△ABC中AB边上的高长=$\frac{3}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$,
故答案为:$\frac{3\sqrt{5}}{5}$.
点评 此题考查了勾股定理,以及三角形的面积,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
5.2014年6月,甲、乙、丙、丁四位备战南京青奥会射击选手在一次训练比赛中,这四位选手各射击10次,每人的平均成绩都是9.5环,方差如下表:
则在这次训练比赛中,这四位选手发挥最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(环2) | 0.35 | 0.018 | 0.22 | 0.055 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.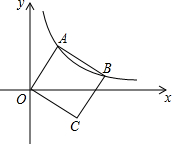 如图,正方形OABC的两顶点A,B恰好在反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上,已知点A坐标为(a,b).
如图,正方形OABC的两顶点A,B恰好在反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上,已知点A坐标为(a,b). 如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为144米2.
如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为144米2.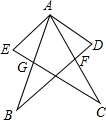 如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.