题目内容
16.下列命题中,属于真命题的是( )| A. | 面积相等的三角形是全等三角形 | |
| B. | 同位角相等 | |
| C. | 若|a|=|b|,则a=b | |
| D. | 如果直线l1∥l2,直线l2∥l3,那么l1∥l3 |
分析 根据全等三角形的判定定理、平行线的性质、绝对值的性质和平行线的传递性对各个选项进行判断即可.
解答 解:两条直角边分别为3和4的直角三角形与两条直角边分别为2和6的直角三角形面积相等但不是全等三角形,A不是真命题;
两直线不平行,同位角不相等,B不是真命题;
|-2|=|2|,-2≠2,C不是真命题;
如果直线l1∥l2,直线l2∥l3,那么l1∥l3,D是真命题
故选:D.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
6.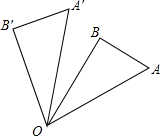 如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
 如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )| A. | n°,1 | B. | n°,2 | C. | n°-30°,1 | D. | n°-30°,2 |
4.已知关于x的方程(x-1)[(k-1)x+(k-3)]=0(k是常数),则下列说法中正确的是( )
| A. | 方程一定有两个不相等的实数根 | B. | 方程一定有两个实数根 | ||
| C. | 当k取某些值时,方程没有实数根 | D. | 方程一定有实数根 |
5.2014年6月,甲、乙、丙、丁四位备战南京青奥会射击选手在一次训练比赛中,这四位选手各射击10次,每人的平均成绩都是9.5环,方差如下表:
则在这次训练比赛中,这四位选手发挥最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(环2) | 0.35 | 0.018 | 0.22 | 0.055 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
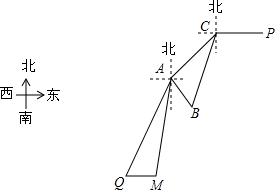 南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.
南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里. 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.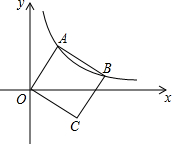 如图,正方形OABC的两顶点A,B恰好在反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上,已知点A坐标为(a,b).
如图,正方形OABC的两顶点A,B恰好在反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上,已知点A坐标为(a,b). 如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE.
如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE.