题目内容
1.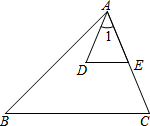 如图,在△ABC中,点E是AC上一点,DE∥BC,∠1=∠B,AD=AE.求证:AB=BC.
如图,在△ABC中,点E是AC上一点,DE∥BC,∠1=∠B,AD=AE.求证:AB=BC.
分析 先根据平行线的性质得∠AED=∠C,加上∠1=∠B,则根据两组角分别对应相等的两三角形相似得到△ADE∽△BAC,则$\frac{AD}{AB}$=$\frac{AE}{BC}$,然后利用AD=AE即可得到结论.
解答 证明:∵DE∥BC,
∴∠AED=∠C,
∵∠1=∠B,
∴△ADE∽△BAC,
∴$\frac{AD}{AB}$=$\frac{AE}{BC}$,
∵AD=AE,
∴AB=BC.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
6.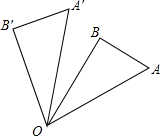 如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
 如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )| A. | n°,1 | B. | n°,2 | C. | n°-30°,1 | D. | n°-30°,2 |
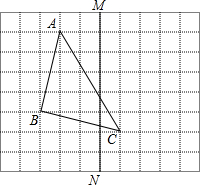 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上. 如图,小明把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,并测得∠1=20°,则∠2的度数是40°.
如图,小明把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,并测得∠1=20°,则∠2的度数是40°.
 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB、BC的中点F、E,四边形OEBF的面积为9,则k=9.