题目内容
2. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.(1)求抛物线的顶点坐标;
(2)若线段AB上有且只有5个点的横坐标为整数,求m的取值范围;
(3)若抛物线在-1<x<0位于x轴下方,在3<x<4位于x轴上方,求m的值.
分析 (1)利用配方法即可解决问题.
(2)由于抛物线y=mx2-2mx+m-3(m>0)的对称轴为直线x=1,线段AB上有且只有5个点的横坐标为整数,于是得到整数为-1,0,1,2,3,列不等式组即可得到结论;
(3)根据抛物线y=mx2-2mx+m-3(m>0)的对称轴为直线x=1,而在3<x<4位于x轴上方,得到抛物线在-2<x<-1这一段位于x轴的上方,根据已知条件得到抛物线过点(-1,0),把(-1,0)代入y=mx2-2mx+m-3即可得到结论.
解答 解:(1)∵y=mx2-2mx+m-3=m(x-1)2-3,
∴抛物线顶点坐标(1,-3);
(2)∵抛物线y=mx2-2mx+m-3(m>0)的对称轴为直线x=1,
线段AB上有且只有5个点的横坐标为整数,这些整数为-1,0,1,2,3,
∴x=2时,y<0;x=4时,y>0;
∴$\left\{\begin{array}{l}{4m-4m+m-3<0}\\{16m-8m+m-3>0}\end{array}\right.$,
解得:$\frac{1}{3}<m<3$;
(3)∵抛物线y=mx2-2mx+m-3(m>0)的对称轴为直线x=1,
而在3<x<4位于x轴上方,
∴抛物线在-2<x<-1这一段位于x轴的上方,
∵在-1<x<0位于x轴下方,
∴抛物线过点(-1,0),
把(-1,0)代入y=mx2-2mx+m-3得m+2m+m-3=0,
解得m=$\frac{3}{4}$.
点评 本题考查了抛物线与x轴的交点,二次函数的图象与系数的关系,正确的理解题意是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.“每天锻炼一小时,健康生活一辈子”,自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了.某校有学生8200人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
14. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )| A. | 66 | B. | 76 | C. | 64 | D. | 100 |
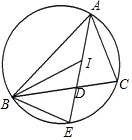 如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.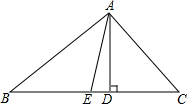 已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,
已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,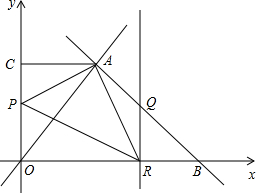 如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.
如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动. 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.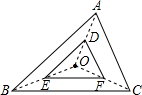 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25.
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25.