题目内容
12.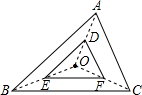 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25.
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25.
分析 根据位似变换的性质得到△DEF∽△ABC,根据题意求出相似比,根据相似三角形的性质解答即可.
解答 解:∵△DEF是由△ABC经过位似变换得到的,
∴△DEF∽△ABC,
∵$\frac{OD}{DA}$=$\frac{2}{3}$,
∴$\frac{OD}{OA}$=$\frac{2}{5}$,即△DEF与△ABC的相似比为$\frac{2}{5}$,
∴△DEF与△ABC的面积比是4:25,
故答案为:4:25.
点评 本题考查的是位似变换的概念、相似三角形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B. 将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形.
将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形. 如图,Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A运动.同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F.联结
如图,Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A运动.同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F.联结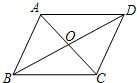 如图,四边形ABCD的对角线交于点O,AB∥CD,O是BD的中点.
如图,四边形ABCD的对角线交于点O,AB∥CD,O是BD的中点.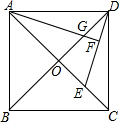 如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.
如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.