题目内容
19.计算:(1)($\sqrt{3-2}$)0+($\frac{1}{3}$)-1+6cos30°-|-$\sqrt{12}$|
(2)已知β是锐角,且:sin(β+15°)=$\frac{\sqrt{3}}{2}$,计算:$\sqrt{8}$-4cosβ-tan45°+tan230°.
分析 (1)原式利用零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果;
(2)利用特殊角的三角函数值求出β的度数,代入原式计算即可得到结果.
解答 解:(1)原式=1+3+3$\sqrt{3}$-2$\sqrt{3}$=4+$\sqrt{3}$;
(2)∵β是锐角,且:sin(β+15°)=$\frac{\sqrt{3}}{2}$,
∴β=45°,
则原式=2$\sqrt{2}$-2$\sqrt{2}$-1+$\frac{1}{3}$=-$\frac{2}{3}$.
点评 此题考查了实数的运算,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.若3am+2b与ab2n-1是同类项,则m+n的值是( )
| A. | -1 | B. | -5 | C. | 2 | D. | 0 |
11.用代数式表示“a的5倍与b的和的平方”,正确的是( )
| A. | (5a+b)2 | B. | 5(a+b)2 | C. | 5a+b2 | D. | (a+5b)2 |
8.已知等腰三角形的周长为12,一边长为5,则它的腰长等于( )
| A. | 5 | B. | 2或5 | C. | 3.5 | D. | 5或3.5 |
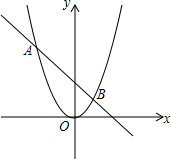 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.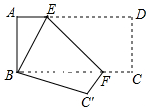 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落到点C′处,折痕为EF.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落到点C′处,折痕为EF.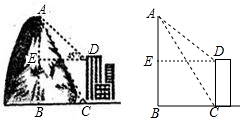 某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)
某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式) 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.