题目内容
11. 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.(1)求证:AD⊥BC;
(2)求AC的长.
分析 (1)先根据三角形中线的定义得出BD=CD=$\frac{1}{2}$BC=5,然后在△ABD中,根据勾股定理的逆定理即可证明AD⊥BC;
(2)由(1)可得∠ADC=90°,再根据勾股定理即可求出AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=13.
解答 (1)证明:∵AD是BC边上的中线,BC=10,
∴BD=CD=$\frac{1}{2}$BC=5.
∵BD2+AD2=52+122=169,
AB2=132=169,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴AD⊥BC;
(2)解:∵AD⊥BC,
∴∠ADC=90°,
∵AD=12,DC=5,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=13.
点评 本题考查了勾股定理及其逆定理,关键是利用勾股定理的逆定理证得AD⊥BC.其中第(2)问也可以利用线段垂直平分线的性质得出AC=AB=13.

练习册系列答案
相关题目
8.已知等腰三角形的周长为12,一边长为5,则它的腰长等于( )
| A. | 5 | B. | 2或5 | C. | 3.5 | D. | 5或3.5 |
6.若a>b,则下列式子正确的是( )
| A. | a-2>b-2 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | 4+3a<4+3b | D. | -2a>-2b |
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.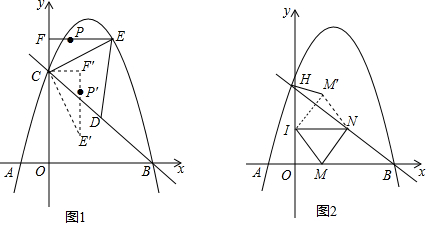
 将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形.
将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形.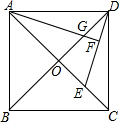 如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.
如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.