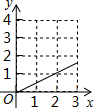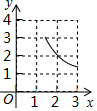题目内容
15.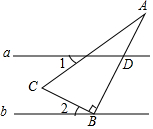 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先根据三角形外角性质,求得∠BDE,进而根据平行线的性质,得到∠DBF=∠BDE=65°,最后根据平角求得∠2.
解答  解:如图所示,∵∠BDE是△ADE的外角,
解:如图所示,∵∠BDE是△ADE的外角,
∴∠BDE=∠3+∠A=∠1+∠A=65°,
∵a∥b,
∴∠DBF=∠BDE=65°,
又∵∠ABC=90°,
∴∠2=180°-90°-65°=25°.
故选:C.
点评 本题考查了平行线的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
5.下列长度的三条线段能组成三角形的是( )
| A. | 2cm,2cm,3cm | B. | 1cm,2cm,3cm | C. | 2cm,3cm,6cm | D. | 5cm,15cm,8cm |
20.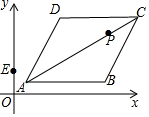 已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
 已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )| A. | (2,2) | B. | (2,$\frac{11}{2}$) | C. | ($\frac{10}{7}$,$\frac{5}{7}$) | D. | ($\frac{9}{4}$,$\frac{13}{8}$) |
4.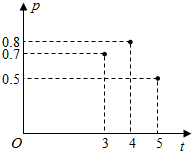 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )| A. | 3.75分钟 | B. | 4.00分钟 | C. | 4.15分钟 | D. | 4.25分钟 |
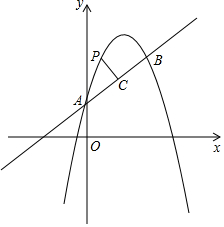 如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+1交于A、B两点,其中点A在y轴上,点B的横坐标是4,P为抛物线上一动点,过点P作PC⊥AB,垂足为点C,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+1交于A、B两点,其中点A在y轴上,点B的横坐标是4,P为抛物线上一动点,过点P作PC⊥AB,垂足为点C,设点P的横坐标为m. 如图,已知菱形ABCD的周长为16cm,AE垂直平分BC,垂足为E
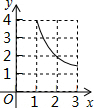
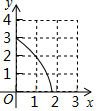
如图,已知菱形ABCD的周长为16cm,AE垂直平分BC,垂足为E 如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )
如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )