题目内容
14. 如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
分析 根据OP的长度不变,始终等于半径,则根据矩形的性质可得OQ=1,再由走过的角度代入弧长公式即可.
解答 解:∵PM⊥AB于点M,PN⊥CD于点N,
∴四边形ONPM是矩形,
又∵点Q为MN的中点,
∴点Q为OP的中点,又OP=2,
则OQ=1,
点Q走过的路径长=$\frac{45π×1}{180}$=$\frac{π}{4}$.
故选A.
点评 本题考查了弧长的计算及矩形的性质,解答本题的关键是根据矩形的性质得出点Q运动轨迹的半径,要求同学们熟练掌握弧长的计算公式.

练习册系列答案
相关题目
4.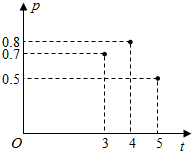 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )| A. | 3.75分钟 | B. | 4.00分钟 | C. | 4.15分钟 | D. | 4.25分钟 |
2.已知△ABC∽△DEF,S△ABC:S△DEF=1:4.若BC=1,则EF的长为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19. 已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
 已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )| A. | m-1 | B. | m+1 | C. | 2n-m+1 | D. | 2n-m-1 |
5.计算(2x-3)2等于( )
| A. | 2x2-6x+9 | B. | 2x2-12x+9 | C. | 4x2-6x+9 | D. | 4x2-12x+9 |
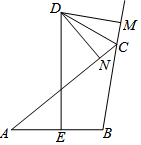 已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.
已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.