题目内容
19.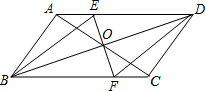 如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.
如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.
分析 由四边形ABCD是平行四边形,即可得AD∥BC,OB=OD,易证得△BEO≌△DFO,可得OE=OF,即可证得四边形BEDF是平行四边形,又由EF⊥BD,即可证得四边形BEDF是菱形.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠BEO=∠DFO,
在△BEO和△DFO中,
$\left\{\begin{array}{l}{∠BEO=∠DFO}\\{∠BOE=∠DOF}\\{OB=OD}\end{array}\right.$,
∴△BEO≌△DFO(AAS),
∴OE=OF,
∴四边形BEDF是平行四边形(对角线互相平分的四边形是平行四边形),
∵EF⊥BD,
∴四边形BEDF是菱形(对角线互相垂直的平行四边形是菱形).
点评 此题考查了平行四边形的判定与性质,菱形的判定以及全等三角形的判定与性质,关键是注意掌握菱形及平行四边形的判定定理.

练习册系列答案
相关题目
9.化简$\frac{{m}^{2}+mn}{{m}^{2}-{n}^{2}}$的结果是( )
| A. | $\frac{2m}{m-n}$ | B. | $\frac{m}{m-n}$ | C. | $\frac{m}{m+n}$ | D. | $\frac{m+n}{m-n}$ |
10.若关于x的一元二次方程ax2+ax+1=0有两个相等的实数根,则a等于( )
| A. | 4 | B. | -4 | C. | 0或4 | D. | 0或-4 |
11.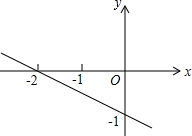 如图,在质地和颜色都相同的三张卡片的正面分别写有-2,-1,1,将三张卡片背面朝上洗匀,从中抽出一张,并记为x,然后从余下的两张中再抽出一张,记为y,则点(x,y)在直线y=-$\frac{1}{2}$x-1上方的概率为( )
如图,在质地和颜色都相同的三张卡片的正面分别写有-2,-1,1,将三张卡片背面朝上洗匀,从中抽出一张,并记为x,然后从余下的两张中再抽出一张,记为y,则点(x,y)在直线y=-$\frac{1}{2}$x-1上方的概率为( )
 如图,在质地和颜色都相同的三张卡片的正面分别写有-2,-1,1,将三张卡片背面朝上洗匀,从中抽出一张,并记为x,然后从余下的两张中再抽出一张,记为y,则点(x,y)在直线y=-$\frac{1}{2}$x-1上方的概率为( )
如图,在质地和颜色都相同的三张卡片的正面分别写有-2,-1,1,将三张卡片背面朝上洗匀,从中抽出一张,并记为x,然后从余下的两张中再抽出一张,记为y,则点(x,y)在直线y=-$\frac{1}{2}$x-1上方的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
 如图,将字母A按箭头所指的方向平移3cm,画出平移后的图形.
如图,将字母A按箭头所指的方向平移3cm,画出平移后的图形. 如图,某校有一块长为(3a+2b)米,宽为(2a+3b)米的长方形地块,规划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=4,b=3时的绿化面积.
如图,某校有一块长为(3a+2b)米,宽为(2a+3b)米的长方形地块,规划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=4,b=3时的绿化面积.