题目内容
8.已知a+x2=2013,b+x2=2014,c+x2=2015,且abc=6012,求$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}$-$\frac{1}{a}-\frac{1}{b}-\frac{1}{c}$的值.分析 原式化为$\frac{(a-b)^{2}+(a-c)^{2}+(b-c)^{2}}{2abc}$,求出a-b=-1,a-c=-2,b-c=-1,代入求值即可.
解答 解:∵$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}$-$\frac{1}{a}-\frac{1}{b}-\frac{1}{c}$
=$\frac{{a}^{2}}{abc}$+$\frac{{b}^{2}}{abc}$+$\frac{{c}^{2}}{abc}$-$\frac{bc}{abc}$-$\frac{ab}{abc}$-$\frac{ab}{abc}$
=$\frac{{a}^{2}+{b}^{2}+{c}^{2}-bc-ac-ab}{abc}$
=$\frac{{2a}^{2}+2{b}^{2}+{2c}^{2}-2bc-2ac-2ab}{2abc}$
=$\frac{(a-b)^{2}+(a-c)^{2}+(b-c)^{2}}{2abc}$,
∵a+x2=2013,b+x2=2014,c+x2=2015,
∴a-b=-1,a-c=-2,b-c=-1,
∴原式=$\frac{1+2+1}{2×6012}$=$\frac{4}{2×6012}$=$\frac{1}{3006}$.
点评 本题考查了分式的化简求值,熟悉统分、完全平方公式是解题的关键.

练习册系列答案
相关题目
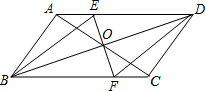 如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.
如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.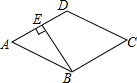 如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE.
如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE.