题目内容
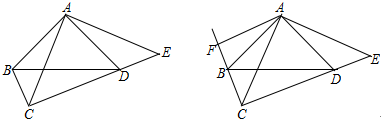
15.如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.(1)求点C的坐标(用字母n表示)(提示:过点C作y轴的垂线)
(2)如果△ABC的面积为5.5,求n的值;
(3)在(2)的条件下,坐标平面内是否存在一点M,使以点M、A、B为顶点组成的三角形与△ABC全等?如果存在画出符合要求的图形,并直接写出点M的坐标.
分析 (1)证明△ABO≌△BCH,得出CH=OB=n,BH=AO=2,即可得出结果;
(2)根据题意列出方程,解方程即可;
(3)分情况讨论:当B为直角顶点时,作M1⊥y轴于E;
当A为直角顶点时,分两种情况:①M2在第二象限时,作M2F⊥x轴于F;②M3在第四象限时,作M4G⊥x轴于G;根据(1)的结果容易求出M的坐标.
解答 解:(1)过点C作y轴的垂线CH,垂足为H,如图所示: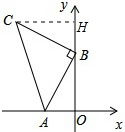
则∠CHB=90°.
∵△ABC是等腰直角三角形,
∴∠ABC=90°,AB=BC,
又∵∠1+∠ABC=∠2+∠CHB,
∴∠1=∠2.
在△ABO和△BCH中,$\left\{\begin{array}{l}∠BHC=∠AOB\\∠1=∠2\\ AB=BC\end{array}\right.$
∴△ABO≌△BCH(AAS),
∴CH=OB=n,BH=AO=2,
点C的坐标是(-n,n+2);
(2)∵S△ABC=S梯形HCAO-S△CHB-S△ABO,∴$5.5=\frac{1}{2}{({n+2})^2}-2n$,解得:$n=\sqrt{7}$(负值已舍),
(3)存在;如图所示: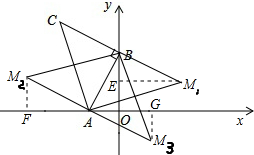 根据题意得M只能为锐角顶点;
根据题意得M只能为锐角顶点;
当B为直角顶点时,作M1⊥y轴于E,
由(1)得,EM1=OB=$\sqrt{7}$,BE=OA=2,
∴OE=$\sqrt{7}$-2,
∴M1($\sqrt{7}$,$\sqrt{7}$-2);
当A为直角顶点时,分两种情况:
①M2在第二象限时,作M2F⊥x轴于F,
由(1)得:M2F=2,AF=$\sqrt{7}$,
∴OF=$\sqrt{7}$+2,
∴M2(-$\sqrt{7}$-2,2);
②M3在第四象限时,作M4G⊥x轴于G,
由(1)得:M3G=2,AG=$\sqrt{7}$,
∴OG=$\sqrt{7}$-2,∴M4($\sqrt{7}$-2,-2);
综上所述:点M的坐标为${M_1}({\sqrt{7},\sqrt{7}-2})$;${M_2}({-\sqrt{7}-2,2})$;${M_3}({\sqrt{7}-2,-2})$.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质以及图形与坐标特征;通过证明三角形全等得出对应边性质是解决问题的关键;要特别注意分类讨论,避免漏解.

 阅读快车系列答案
阅读快车系列答案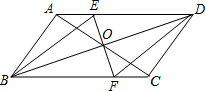 如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.
如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别相交于点E、F,求证:四边形BEDF是菱形.