题目内容

15．求式子（m-2n+3）（m-2n-3）+9的平方根．

分析 把原式的第一项中的两因式中的m-2n结合，发现满足平方差公式的特点，故利用平方差公式化简，合并后把原式化为一个数的完全平方形式，即可求出原式的平方根．

解答 解：（m-2n-3）（m-2n+3）+9
=[（m-2n）-3][（m-2n）+3]+9
=（m-2n）2-32+9
=（m-2n）2，
故式子（m-2n+3）（m-2n-3）+9的平方根为±（m-2n）．

点评 此题考查了整式的混合运算，涉及的知识有：平方差公式，二次根式的化简公式，以及绝对值的代数意义，是中考中常考的题型．

练习册系列答案
相关题目
5．解方程组：$\left\{\begin{array}{l}x+y+z=2\\ 4x+2y+z=4\\ 2x+3y+z=1.\end{array}\right.$．
6．如图，D、E分别是等边△ABC的边AC、BC所在直线上的两点，且AD=CE，连BD、DE．
（1）如图1，D在线段AC上，E在线段BC的延长线上；
①求证：DB=DE；②作DH⊥BC于H，∠BDE=90°，求证：BD=$\sqrt{2}$DH；
（2）如图2，D在线段CA的延长线上，E在线段BC上，DE交AB于F点，∠CDE=15°，求证：BD=$\sqrt{2}$BF；
（3）如图3，D在线段AC上，E在线段BC的延长线上，且CD=2CE，S△ABC=8，请直接写出△BDE的面积为$\frac{64}{9}$．
3．平面上有六个点，每两个点都连成一条直线，问除了原来的6个点之外，这些直线最多还有（　　）个交点．
A．35B．40C．45D．55
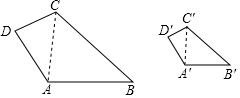10．如图，四边形ABCD与四边形A′B′C′D′相似．
（1）连接相应的对角线AC，A′C′所得的△ABC与△A′B′C′相似吗？△ACD与△A′C′D′呢？如果相似，它们的相似比相等吗？为什么？
（2）四边形ABCD与四边形A′B′C′D′的周长比、面积比与相似比有什么关系？
如果两个五边形相似，还有相同的结论吗？
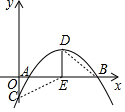20．关于x的二次函数y=-（x-e）2+$\frac{1}{4}$中．e＞$\frac{1}{2}$是常数，其函数图象如图所示．点D是二次函数图象的顶点，DE⊥x轴，E是垂足．二次函数图象交x轴于点A、B（A在B左侧），交y轴于点C．
（1）求点A、B、C、D的坐标．（用e表示）；
（2）若以O、C、E为顶点的三角形与△DEB相似，求e的值．
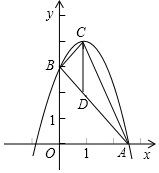7．如图，抛物线y=-x2+2x+3顶点坐标为点C，交x轴正半轴于点A，交y轴于点B，点P是抛物线（在第一象限内）上的一个动点，连接PA，PB．
（1）求直线AB的解析式；
（2）当P点运动到顶点C时，CD∥OB交AB于D，求S△CAB；
（3）是否存在一点P，使S△PAB=$\frac{9}{8}$S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．
4．在一个不透明的袋子中装有三个完全相同的小球，分别标有数字1，2，-4从袋子中随机取出一个小球，用小球上的数字作为x（不放回），再取出一个小球，用小球上的数字作为y，确定一个点的坐标为（x，y）．
（1）请用列表法或者画树状图法表示点的坐标的所有可能结果；
（2）求满足x+y＜0的概率．
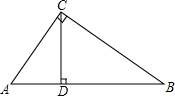5．已知CD是Rt△ABC斜边上的高，AB=5，BC=4，求：S△ABC：S△ACD：S△BCD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网