题目内容
3.平面上有六个点,每两个点都连成一条直线,问除了原来的6个点之外,这些直线最多还有( )个交点.| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
分析 先求出平面上六个点一共有1+2+3+4+5=15条直线,进一步得到这些直线最多共有15×14÷2=105个交点,原来的6个点每个点都通过5条直线,充当了6×5×4÷2=60个交点,两者相减即可求解.
解答 解:一共有1+2+3+4+5=15条直线,
这些直线最多共有15×14÷2=105个交点,
其中原来的6个点每个点都通过5条直线,充当了6×5×4÷2=60个交点,
于是剩余的交点最多有105-60=45个.
故这些直线最多还有45个交点.
故选:C.
点评 考查了直线、射线、线段,本题可以按握手问题去解答,要注意去掉重复计算的情况,如果直线条数少可以用枚举法解答,如果直线条数比较多可以用公式:交点数=n(n-1)÷2解答.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.下列各数中,能使不等式x-1>0成立的是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -2 |
 如图,有一个面积为20的矩形,它的两邻边分别为x、y(2≤x≤10),则y与x的函数图象大致是( )
如图,有一个面积为20的矩形,它的两邻边分别为x、y(2≤x≤10),则y与x的函数图象大致是( )



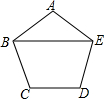 已知如图,正五边形ABCDE的边长为6.
已知如图,正五边形ABCDE的边长为6. 如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
如图所示,求∠A+∠B+∠C+∠D+∠E的度数. 如图,已知△ABC≌△ADC,∠BAD=120°,∠ACD=25°,则∠D=95°.
如图,已知△ABC≌△ADC,∠BAD=120°,∠ACD=25°,则∠D=95°.