题目内容
10．
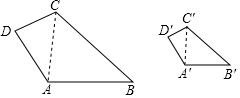如图，四边形ABCD与四边形A′B′C′D′相似．（1）连接相应的对角线AC，A′C′所得的△ABC与△A′B′C′相似吗？△ACD与△A′C′D′呢？如果相似，它们的相似比相等吗？为什么？
（2）四边形ABCD与四边形A′B′C′D′的周长比、面积比与相似比有什么关系？
如果两个五边形相似，还有相同的结论吗？
分析 （1）直接利用相似多边形的性质得出对应边的比以及对应角相等，进而得出答案；
（2）直接利用相似三角形的性质得出相似多边形的性质．
解答 解：（1）∵四边形ABCD与四边形A′B′C′D′相似，
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CD}{C′D′}$=$\frac{AD}{A′D′}$，∠D=∠D′，∠B=∠B′，
∴△ABC∽△A′B′C′，△ACD∽△A′C′D′，
且相似比相等；
（2）四边形ABCD与四边形A′B′C′D′的周长比等于相似比，面积比为相似比的平方，
五边形还有相同的结论．
点评 此题主要考查了相似多边形的性质，正确把握相似图形的性质是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
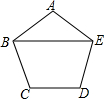已知如图，正五边形ABCDE的边长为6．
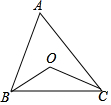如图，在△ABC中，∠ABC、∠ACB的平分线交于点O．
在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．求证：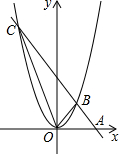
如图，直线l过x轴上一点A（2，0），且与抛物线y=ax2相交于B，C两点，B点坐标为（1，1）．