题目内容
5.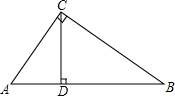 已知CD是Rt△ABC斜边上的高,AB=5,BC=4,求:S△ABC:S△ACD:S△BCD.
已知CD是Rt△ABC斜边上的高,AB=5,BC=4,求:S△ABC:S△ACD:S△BCD.
分析 根据勾股定理和三角形的面积进行解答即可.
解答 解:∵CD是Rt△ABC斜边上的高,AB=5,BC=4,
∴AC=$\sqrt{{5}^{2}-{4}^{2}}=3$,
∴S△ABC=$\frac{1}{2}×3×4=\frac{1}{2}×5×CD$,
∴CD=$\frac{12}{5}$,
∴$\frac{AD}{\frac{12}{5}}=\frac{3}{4}$,
∴AD=$\frac{9}{5}$,
∴BD=$5-\frac{9}{5}=\frac{16}{5}$,
∴S△ABC:S△ACD:S△BCD=$\frac{1}{2}×3×4:\frac{1}{2}×\frac{9}{5}×\frac{12}{5}:\frac{1}{2}×\frac{16}{5}×\frac{12}{5}$=25:9:16.
点评 本题主要考查了勾股定理以及三角形的面积的知识,解题的关键是熟练使用勾股定理和三角形的面积,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列各运算中,正确的是( )
| A. | 3a+2a=5a2 | B. | (x-3y)2=$\frac{y^2}{x^6}$ | C. | a6÷a2=a3 | D. | (a+2)2=a2+4 |
 如图,已知△ABC≌△ADC,∠BAD=120°,∠ACD=25°,则∠D=95°.
如图,已知△ABC≌△ADC,∠BAD=120°,∠ACD=25°,则∠D=95°.
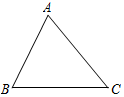 如图,把△ABC绕点C顺时针旋转40°后,得到△A′B′C,其中点A、B分别与点A′、B′对应,且点B′落在边AB上,A′B′与边AC相交于点D,如果∠A′DC=90°,那么∠A=50度.
如图,把△ABC绕点C顺时针旋转40°后,得到△A′B′C,其中点A、B分别与点A′、B′对应,且点B′落在边AB上,A′B′与边AC相交于点D,如果∠A′DC=90°,那么∠A=50度.