题目内容
7.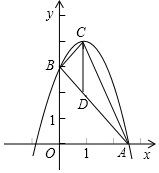 如图,抛物线y=-x2+2x+3顶点坐标为点C,交x轴正半轴于点A,交y轴于点B,点P是抛物线(在第一象限内)上的一个动点,连接PA,PB.
如图,抛物线y=-x2+2x+3顶点坐标为点C,交x轴正半轴于点A,交y轴于点B,点P是抛物线(在第一象限内)上的一个动点,连接PA,PB.(1)求直线AB的解析式;
(2)当P点运动到顶点C时,CD∥OB交AB于D,求S△CAB;
(3)是否存在一点P,使S△PAB=$\frac{9}{8}$S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.
分析 (1)根据抛物线解析式求得A、B的坐标,然后利用待定系数法确定函数关系式;
(2)C点坐标为(1,4),根据三角形的面积公式即可求解;
(3)根据S△PAB=$\frac{9}{8}$S△CAB即可得到一个关于点P的横坐标的方程,即可求出x的值.进而得到P点的坐标.
解答  解:①∵抛物线y=-x2+2x+3,
解:①∵抛物线y=-x2+2x+3,
∴当y=0时,x1=-1,x2=3.
当x=0时,y=3;
∴如图所示,A(3,0),B(0,3).
设直线AB的解析式为:y=kx+b(k≠0),
把A(3,0),B(0,3)代入,得$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
所以直线AB的解析式为:y=-x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴C点坐标为(1,4)
∴当x=1时,y1=4,y2=2,
∴CD=4-2=2,S△CAB=$\frac{1}{2}$×3×2=3;
(3)假设存在符合条件的点P,设点P的横坐标是x,△PAB的铅垂高为h,
则h=y1-y2=(-x2+2x+3)-(-x+3)=-x2+3x(8分)
由S△PAB=$\frac{9}{8}$S△CAB
得:$\frac{1}{2}$×3×(-x2+3x)=$\frac{9}{8}$×3,化简得:4x2-12x+9=0
解得,x=$\frac{3}{2}$,
将x=$\frac{3}{2}$代入y1=-x2+2x+3中,
解得P点坐标为( $\frac{3}{2}$,$\frac{15}{4}$).
点评 主要考查了二次函数综合题,需要学生掌握二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

 一课一练课时达标系列答案
一课一练课时达标系列答案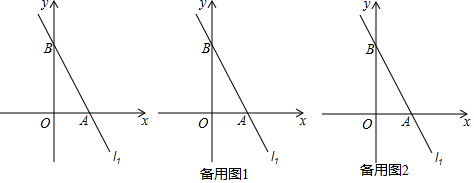
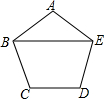 已知如图,正五边形ABCDE的边长为6.
已知如图,正五边形ABCDE的边长为6. 在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:
在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证: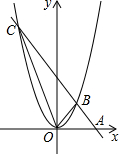 如图,直线l过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点坐标为(1,1).
如图,直线l过x轴上一点A(2,0),且与抛物线y=ax2相交于B,C两点,B点坐标为(1,1).