题目内容
19. 如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移3个单位长度与y轴首次相切,得到⊙A′,并画出⊙A′.此时点A′的坐标为(2,1).
(3)求BC的长.
分析 (1)根据点A坐标画出坐标系即可.
(2)观察图象即可解决问题.
(3)连接AC,过点A作AD⊥BC于点D,利用勾股定理即可解决.
解答 解:(1)坐标系如图所示,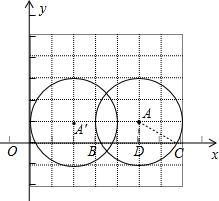
(2)⊙A向左平移3个单位长度与y轴首次相切,此时点A′坐标(2,1).
故答案分别为3,(2,1).
(3)连接AC,过点A作AD⊥BC于点D.
则BC=2DC,
由A(5,1)可得AD=1,
又∵AC=2,
∴在Rt△ADC中,DC=$\sqrt{A{C^2}-A{D^2}}=\sqrt{{2^2}-{1^2}}=\sqrt{3}$
∴BC=2$\sqrt{3}$.
点评 本题考查坐标与图形、切线的性质、垂径定理、勾股定理、平移等知识,解题的关键是正确画出图形,添加辅助线构造直角三角形解决问题.属于中考常考题型.

练习册系列答案
相关题目
13.若a、b为实数,且满足$|{a-2}|+\sqrt{3-b}=0$,则b-a的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | 以上都不对 |
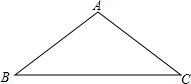 如图,在△ABC中,AB=AC=10,BC=16.
如图,在△ABC中,AB=AC=10,BC=16. 如图,有一圆经过△ABC的三个顶点,且线段BC的垂直平分线与圆弧$\widehat{AC}$相交于D点,连结CD、AD,若∠B=74°,∠ACB=52°,则∠BAD=117°.
如图,有一圆经过△ABC的三个顶点,且线段BC的垂直平分线与圆弧$\widehat{AC}$相交于D点,连结CD、AD,若∠B=74°,∠ACB=52°,则∠BAD=117°. 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.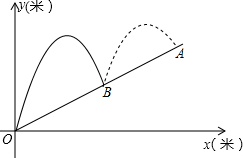 如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上)
如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上) 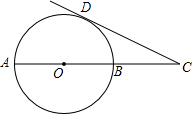 如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.
如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.