题目内容
4.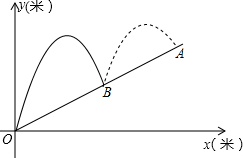 如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上)
如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上) (1)求山坡OA的解析式;
(2)求出点B的坐标;
(3)已知OA=8$\sqrt{5}$m,那么第二杆能否打进球洞A?
分析 (1)设B(2a,a),OA的解析式为y=kx,于是得到a=2ak即可得到结论;
(2)由抛物线y=-$\frac{1}{4}$(x+h)2+9过(0,0)点,得到方程求得h=-6,解方程组即可得到结论;
(3)点B在第二段抛物线上,得到-$\frac{1}{4}$(10+h)2=5,求得h=-14,解方程组得到A(16,8),根据勾股定理得到OA=$\sqrt{1{6}^{2}+{8}^{2}}$=8$\sqrt{5}$,于是得到结论.
解答 解:(1)设B(2a,a),OA的解析式为y=kx,
∴a=2ak
k=$\frac{1}{2}$
∴OA的解析式为y=$\frac{1}{2}$x;
(2)∵抛物线y=-$\frac{1}{4}$(x+h)2+9过(0,0)点,
∴-$\frac{1}{4}$(0+h)2+9=0,解得h=±6,
∵抛物线开口向下,对称轴在y轴右侧,
∴h=-6,
解$\left\{\begin{array}{l}{y=-\frac{1}{4}(x-6)^{2}+9}\\{y=\frac{1}{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{1}=10}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=0}\end{array}\right.$(舍去),
∴B(10,5),
(3)点B在第二段抛物线上,
∴-$\frac{1}{4}$(10+h)2+9=5,
∴h=-14,
依题意有$\left\{\begin{array}{l}{y=-\frac{1}{4}(x-14)^{2}+9}\\{y=\frac{1}{2}x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=16}\\{{y}_{1}=8}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=10}\\{{y}_{2}=5}\end{array}\right.$(舍去),
∴A(16,8),
∴OA=$\sqrt{1{6}^{2}+{8}^{2}}$=8$\sqrt{5}$,
∴第二杆能打进球洞A.
点评 本题考查了二次函数的应用及解直角三角形的知识,涉及了待定系数法求函数解析式的知识,注意建立数学模型,培养自己利用数学知识解决实际问题的能力,难度一般.

①f(a,b)=(-a,b).如:f(1,3)=(-1,3);
②g(a,b)=(b,a).如:g(1,3)=(3,1);
③h(a,b)=(-a,-b).如,h(1,3)=(-1,-3).
按照以上变换有:f(g(h(2,-3)))=f(g(-2,3))=f(3,-2)=(-3,-2),
那么f(g(h(-3,5)))等于( )
| A. | (-5,-3) | B. | (5,3) | C. | (5,-3) | D. | (-5,3) |
 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.| A. | 8$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
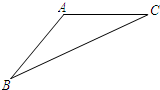 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC. 如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题: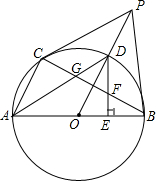 如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G
如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G