题目内容
11.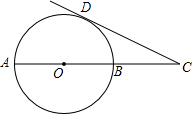 如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.
如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.
分析 连接OD,根据切线的性质,∠ODC=90°,设OD=r,在RT△ODC中利用勾股定理即可解决.
解答 解: 连接OD.
连接OD.
∵CD是⊙O切线,
∴OD⊥CD,
∴∠ODC=90°,设半径为r,
在RT△ODC中,∵OD=r,OC=r+2,CD=4,
∴OD2+CD2=OC2,
∴r2+42=(r+2)2,
∴r=3,
∴⊙O的半径为3.
点评 本题考查切线的性质、勾股定理等知识,解题的关键是利用勾股定理,把问题转化为方程解决,属于中考常考题型.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
1.下列计算正确的是( )
| A. | b5•b5=2b5 | B. | (an-1)3=a3n-1 | C. | a+2a2=3a3 | D. | (a-b)5(b-a)4=(a-b)9 |
6.下列运算正确的是( )
| A. | (-a3)2=-a6 | B. | a8÷a4=a2 | C. | (a-b)2=a2-b2 | D. | a2•a3=a5 |
 如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题: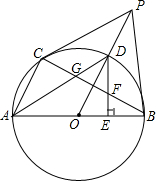 如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G
如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G