题目内容
3. 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
分析 过E作EN⊥DC,可证得△BCG≌△DCE,从而可得到∠EDC=∠CBM,可证明△BCM∽△DNE∽△DHM,得出M为CD的中点,进一步求得BM和BH,可求得BH的长.
解答 解:过E作EN⊥DC,垂足为N,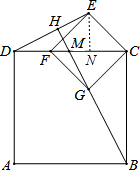
∵CE=2$\sqrt{2}$,四边形CEFG为正方形,
∴FC=4,
∵N为FC的中点,
∴DN=4,
∴EN:DN:DE=1:2:$\sqrt{5}$,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{CB=CD}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴∠EDC=∠CBM,
∴△BCM∽△DNE∽△DHM,
∴M为CD的中点,
∴BM=$\sqrt{5}$MC=3$\sqrt{5}$,HM=$\frac{DM}{\sqrt{5}}$=$\frac{3}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$,
∴BH=BM+HM=3$\sqrt{5}$+$\frac{3\sqrt{5}}{5}$=$\frac{18\sqrt{5}}{5}$.
故答案为:$\frac{18\sqrt{5}}{5}$.
点评 本题主要考查相似三角形的判定和性质及正方形的性质,利用相似三角形的性质证得M为CD的中点,求出BM和HM是解题的关键.

练习册系列答案
相关题目
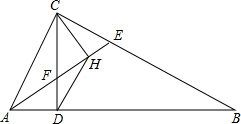 △ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:
△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证: 如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.
如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.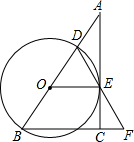 如图,在Rt△ABC中,∠ACB=90°,点D是AB边上的一点,以BD为直径作⊙O,过O作AC的垂线交AC于点E,恰好垂足E在⊙O上,连接DE并延长DE交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点D是AB边上的一点,以BD为直径作⊙O,过O作AC的垂线交AC于点E,恰好垂足E在⊙O上,连接DE并延长DE交BC的延长线于点F.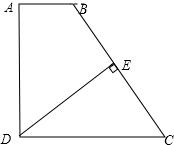 如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.
如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.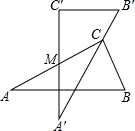 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.