题目内容
15.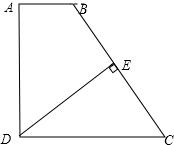 如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.
如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.
分析 结论CD2=AD2+AB2,根据垂直平分线的性质,得到DB=DC,在RT△ABD中利用勾股定理即可证明.
解答 解:结论CD2=AD2+AB2,理由如下:
∵DE⊥BC,BE=EC,
∴DB=DC,
∵四边形ABCD是直角梯形,
∴∠A=90°,
在RT△ABD中,∵AD2+AB2=BD2,
∴AD2+AB2=CD2.
点评 本题考查线段垂直平分线的性质、勾股定理、直角梯形的性质等知识,利用垂直平分线的性质是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
7.A、B两乡分别由大米200吨、300吨.现将这些大米运至C、D两个粮站储存.已知C粮站可储存240吨,D粮站可储存260吨,从A乡运往C、D两处的费用分别为每吨20元和25元,B乡运往C、D两处的费用分别为每吨15元和18元.设A乡运往C粮站大米x吨.A、B两乡运往两个粮站的运费分别为yA、yB元.
(1)请填写下表,并求出yA、yB与x的关系式:
(2)试讨论A、B乡中,哪一个的运费较少;
(3)若B乡比较困难,最多只能承受4830元费用,这种情况下,运输方案如何确定才能使总运费最少?最少的费用是多少?
(1)请填写下表,并求出yA、yB与x的关系式:
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
(3)若B乡比较困难,最多只能承受4830元费用,这种情况下,运输方案如何确定才能使总运费最少?最少的费用是多少?
5. 如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )
如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )
 如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )
如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )| A. | 70° | B. | 60° | C. | 55° | D. | 110° |

 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.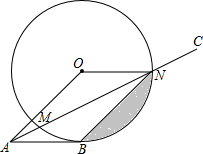 如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm. 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.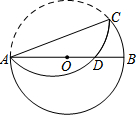 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.