题目内容
6. 如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.
如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.
分析 ①延长AE、BC交于点M,求出∠DAE=∠CME,AB=BM,根据ASA推出△ADE≌△MCE,根据全等得出AE=EM,∠DAE=∠M,求出∠M=∠BAE,推出AB=BM,根据等腰三角形的性质得出即可.
②过E作EF⊥AB于F,根据角平分线性质得出EF=DE,推出EF=CE,根据角平分线性质得出即可.
解答 ①解:如图1中.延长AE、BC交于点M
∵AD∥BC
∴∠DAE=∠CME,
∵AE平分∠BAD,
∴∠DAE=∠BAM,
∴∠BAM=∠CME,
∴AB=BM,
在△ADE和△MCE中,
$\left\{\begin{array}{l}{∠D=∠ECM}\\{DE=CE}\\{∠AED=∠CEM}\end{array}\right.$,
∴△ADE≌△MCE,
∴AE=EM,∠DAE=∠M
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠M=∠BAE,
∴AB=BM,
∵AE=EM,
∴BE⊥AM.
②证明:如图2中,过E作EF⊥AB于F,
∵∠D=90°,AE平分∠BAD,
∴EF=DE,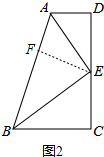
∵E为DC中点
∴DE=EC,
∴EF=EC,
∵EF⊥AB,∠C=90°,
∴BE平分∠ABC;
点评 本题主要考查了全等三角形的判定与性质、等腰三角形的性质、角平分线的判定和性质等知识,添加辅助线是解题的关键,属于中考常考题型.

练习册系列答案
相关题目
14.对于抛物线y=x2+2和y=x2的论断:①开口方向不同;②形状完全相同;③对称轴相同.其中正确的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.某商场计划购进A、B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
(1)若商场预计进货款为3900元,则这两种台灯各购进多少盏?
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 55 |
| B型 | 50 | 70 |
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
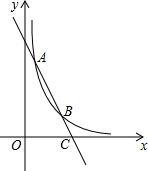 如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.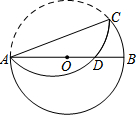 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.