题目内容
13.盱眙第一山景区为提高某景点的安全性,决定将到达景点的步行台阶进行改善,把倾角由45°减至30°,已知原台阶坡面AB的长为5m(BC所在地面为水平面)(1)改善后的台阶坡面会加长多少?(就是问AD比AB长多少?)
(2)改善后的台阶多占多长一段水平地面?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)(就是求BD的长)
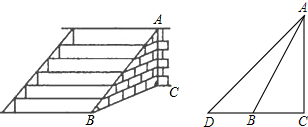
分析 (1)要求改善后的台阶坡面会加长多少,只要求出AD的长,然后AD与AB作差即可,要求AD的长,根据AB和∠ABC可以求得AC的长,然后根据AC和∠ADC的度数即可求得AD,本题得以解决;
(2)要求改善后的台阶多占多长一段水平地面,只要求的DC和BC的长,然后DC和BC作差即可,要求BC,根据AB和∠ABC可以求得,要求DC可以根据第一问求得的AC的长和∠ADC求得,本题得以解决.
解答 解:(1)∵由题意可得,AB=5m,∠ABC=45°,∠ADC=30°,
∴AC=AB•sin45°=5×$\frac{\sqrt{2}}{2}=\frac{5\sqrt{2}}{2}$,
∴AD=$\frac{AC}{sin30°}=\frac{\frac{5\sqrt{2}}{2}}{\frac{1}{2}}=5\sqrt{2}$,
∴AD-AB=($5\sqrt{2}-5$)m,
即改善后的台阶坡面会加长($5\sqrt{2}-5$)m;
(2)∵由题意可得,AB=5m,∠ABC=45°,∠ADC=30°,
∴BC=AB•cos45°=5×$\frac{\sqrt{2}}{2}=\frac{5\sqrt{2}}{2}$,AC=AB•sin45°=5×$\frac{\sqrt{2}}{2}=\frac{5\sqrt{2}}{2}$,
∴CD=$\frac{AC}{tan30°}=\frac{\frac{5\sqrt{2}}{2}}{\frac{\sqrt{3}}{3}}=\frac{5\sqrt{6}}{2}$,
∴CD-BC=$\frac{5\sqrt{6}}{2}-\frac{5\sqrt{2}}{2}$=$\frac{5\sqrt{6}-5\sqrt{2}}{2}=\frac{5\sqrt{2}(\sqrt{3}-1)}{2}$≈$\frac{5×1.41×(1.73-1)}{2}$≈2.6m,
即改善后的台阶多占2.6m长的一段水平地.
点评 本题考查解直角三角形的应用--坡度坡角问题,解题的关键是明确题意,找出所求问题需要的条件,利用特殊角的三角函数值进行解答.

| A. | 5a+a=5a2 | B. | 5a+b=5ab | C. | 5a2b-3ab2=2a2b | D. | 2ab2-5b2a=-3ab2 |
 如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )
如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=110°,则∠D等于( )| A. | 70° | B. | 60° | C. | 55° | D. | 110° |
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.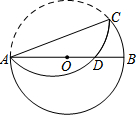 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.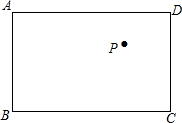 如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$. 如图,已知AB⊥BD,CD⊥BD.
如图,已知AB⊥BD,CD⊥BD.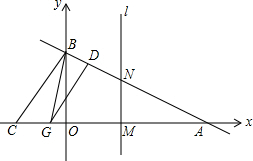 已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.
已知:如图,直线y=-$\frac{1}{2}$x+4与x轴交于A点,与y轴交于B点.点C是x轴负半轴上的一点,且满足OC:BC=3:5.