题目内容
13. 如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )
如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )| A. | 4 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
分析 先根据∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,求出边BA的长度,再根据该图形为中心对称图形得出BA=B′A,然后由BB′=BA+B′A求解即可.
解答 解:∵∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,
∴根据勾股定理可得:BA=$\sqrt{{{AC}^{2}+BC}^{2}}$=$\sqrt{\frac{1}{3}+1}$=$\frac{2\sqrt{3}}{3}$,
∵该图形为中心对称图形,
∴BA=B′A,
∴BB′=BA+B′A=2×$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
故选D.
点评 本题考查了中心对称图形和勾股定理的知识,解答本题的关键在于熟练掌握中心对称图形的概念和勾股定理的运算法则.

练习册系列答案
相关题目
3.在数轴上表示不等式x+6≥2的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
8. 如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
 如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )
如图:AB∥CD,直线MN与AB交于E,过点E作直线HE⊥MN,∠1=130°,则∠2等于( )| A. | 50° | B. | 40° | C. | 30° | D. | 60° |
3.已知α为锐角,且sin(α-10°)=$\frac{\sqrt{2}}{2}$,则α等于( )
| A. | 45° | B. | 55° | C. | 60° | D. | 65° |
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论: 如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F.
如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F.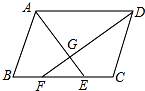 如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.