题目内容
2.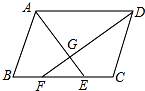 如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.(1)求证:∠AGD=90°.
(2)若CD=4cm,求BE的长.
分析 (1)由平行四边形的性质和角平分线即可得出结论;
(2)利用平行四边形的性质结合角平分线的性质得出∠BAE=∠BEA,∠CFD=∠CDF,进而求出AB=BE=CD=4cm即可.
解答 (1)证明:∵四边形ABCCD是平行四边形,
∴∠BAD+∠ADC=180°,
∵AE、DF分别是∠BAD、∠ADC的平分线,
∴∠DAG=$\frac{1}{2}$∠BAD,∠ADG=$\frac{1}{2}$∠ADC,
∴∠DAG+∠ADG=$\frac{1}{2}$×(∠BAD+∠ADC)=$\frac{1}{2}$×180°=90°,
∴∠AGD=90°;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∵CD=4cm,
∴BE=4cm,
点评 此题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,得出AB=BE是解决问题(2)的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
13. 如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )
如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )
 如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )
如图是一个中心对称图形,A为对称中心,若∠C=90°,AC=$\frac{\sqrt{3}}{3}$,BC=1,则BB′长为( )| A. | 4 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
7.今年“五一”小黄金周期间,我市旅游公司组织50名游客分散到A、B、C三个景点游玩.三个景点的门票价格如表所示:
所购买的50张票中,B种票张数是A种票张数的3倍还多1张,设需购A种票张数为x,C种票张数为y.
(1)写出y与x之间的函数关系式;
(2)设购买门票总费用为w(元),求出w与x之间的函数关系式;
(3)若每种票至少购买1张,且A种票不少于10张,则共有几种购票方案?并求出购票总费用最少时,购买A、B、C三种票的张数.
| 景点 | A | B | C |
| 门票单价(元) | 30 | 55 | 75 |
(1)写出y与x之间的函数关系式;
(2)设购买门票总费用为w(元),求出w与x之间的函数关系式;
(3)若每种票至少购买1张,且A种票不少于10张,则共有几种购票方案?并求出购票总费用最少时,购买A、B、C三种票的张数.
11.方程6+3x=0的解是( )
| A. | x=-2 | B. | x=-6 | C. | x=2 | D. | x=6 |

 如图,平面直角坐标系中,已知A(0,2),B(2,2),C(1,1).
如图,平面直角坐标系中,已知A(0,2),B(2,2),C(1,1).