题目内容
14.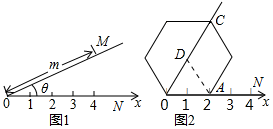 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
| A. | (4,60°) | B. | (4,45°) | C. | (2$\sqrt{2}$,60°) | D. | (2$\sqrt{2}$,50°) |
分析 设正六边形的中心为D,连接AD,判断出△AOD是等边三角形,根据等边三角形的性质可得OD=OA,∠AOD=60°,再求出OC,然后根据“极坐标”的定义写出即可.
解答  解:如图,设正六边形的中心为D,连接AD,
解:如图,设正六边形的中心为D,连接AD,
∵∠ADO=360°÷6=60°,OD=AD,
∴△AOD是等边三角形,
∴OD=OA=2,∠AOD=60°,
∴OC=2OD=2×2=4,
∴正六边形的顶点C的极坐标应记为(4,60°).
故选A.
点评 本题考查了正多边形和圆,坐标确定位置,主要利用了正六边形的性质,读懂题目信息,理解“极坐标”的定义是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
6. 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
 如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )
如图,AB,CD是⊙O的两条弦,连接AD,BC,若∠BCD=50°,则∠BAD的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
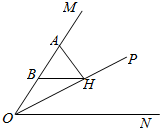 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.