题目内容
2.已知:a是-2的相反数,b是-2的倒数,则(1)a=2,b=-$\frac{1}{2}$;
(2)求代数式a2b+ab的值.
分析 (1)根据相反数和倒数定义得出即可;
(2)先分解因式,再代入求出即可.
解答 解:(1)∵a是-2的相反数,b是-2的倒数,
∴a=2,b=-$\frac{1}{2}$,
故答案为:2,-$\frac{1}{2}$;
(2)当a=2,b=-$\frac{1}{2}$时,a2b+ab=ab(a+1))=2×(-$\frac{1}{2}$)×(2+1)=-3.
点评 本题考查了求代数式的值,相反数和倒数等知识点,能求出a、b的值是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
 雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )
雷达二维平面定位的主要原理是:测量目标的两个信息--距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标B的位置表示为F(4,150°).用这种方法表示目标C的位置,正确的是( )| A. | (-3,300°) | B. | (3,60°) | C. | (3,300°) | D. | (-3,60°) |
14.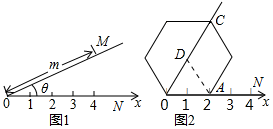 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
| A. | (4,60°) | B. | (4,45°) | C. | (2$\sqrt{2}$,60°) | D. | (2$\sqrt{2}$,50°) |
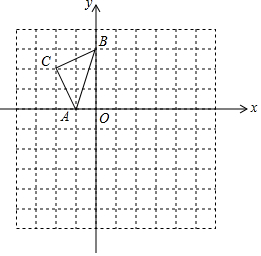 如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).